11 Recursion Function Examples for Practice (Easiest 😎 to Hardest🤯)

If you are new to Python and struggle to get your hands dirty with Recursive functions, you must try to solve the problems listed in this article. The article is sorted from easy to challenging levels. By solving each problem, you get ready and confident to solve the next challenge. Let’s dive in 🤿

Recursive Function Explained – Understand recursion with functions in Python intuitively.

Factorial of a Number

In the “Introduction to the Recursive function” blog, you will learn recursive functions with the factorial problem.

Fibonacci Sequence

The most famous formulas in mathematics are the Fibonacci sequence. Each number in the sequence is the sum of the two numbers that precede it. Therefore, sequence looks like: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on.

Fn = Fn-1 + Fn-2

with seed values

F0 = 0 and F1 = 1

Both factorial and Fibonacci are what we call Primitive Recursions, which means that we can also do them in “for” loops. However, there are some functions that are completely recursive, i.e we must do them recursively.

def fib(n) : if n==0 : return 0 elif n ==1 : return 1 else : return fib(n-1) +fib(n-2) print(fib(7))

Sum of Digits of a Number

It is used to find the sum of digits of a number using recursion.

def sumDigits(no): if no == 0: return 0 else : return int(no % 10) + sumDigits(int(no / 10)) print(sumDigits(123))

Sum of the First n Natural Numbers

In this problem, we are simply adding 1 to n natural numbers.

Likewise, we can find the sum of odd or even numbers.

def sumnums(n): if n == 1: return 1 return n + sumnums(n - 1) print(sumnums(3)) print(sumnums(6)) print(sumnums(9))

Power of a Number

The product of multiplying a number by itself is called Power. Usually, with a Base number and an Exponent, the Power is expressed. The exponent refers to a small number written above and to the right of the base number. It depicts how many times the base number is multiplied.

def power(num, topwr): if topwr == 0: return 1 else: return num * power(num, topwr - 1) print('{} to the power of {} is {}'.format(4, 7, power(4, 7))) print('{} to the power of {} is {}'.format(2, 8, power(2, 8)))

Least Common Multiple(LCM) of 2 Numbers

The least common multiple(LCM) of a number is the smallest number that is the product of two or more numbers.

def LCM(a, b): t = a % b if t == 0: return a return a * LCM(b, t) / t print(LCM(2, 5))

Greatest Common Divisor(GCD) of 2 Numbers

The most significant positive number is the GCD of two or more integers that each of the integers is divisible, i.e., it is the most significant number that divides both of them. Thus, simply factorizing both numbers and multiplying common prime factors will give GCD.

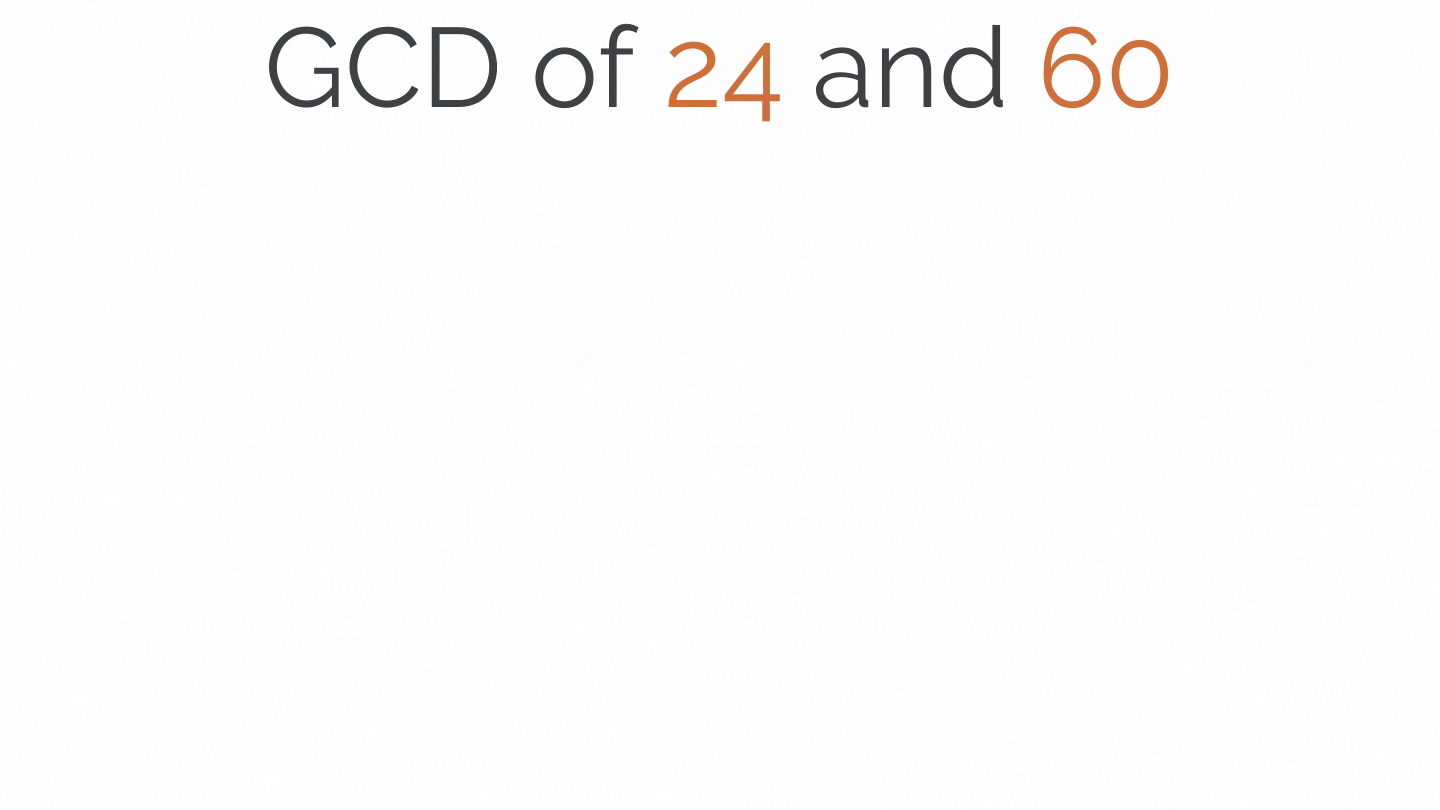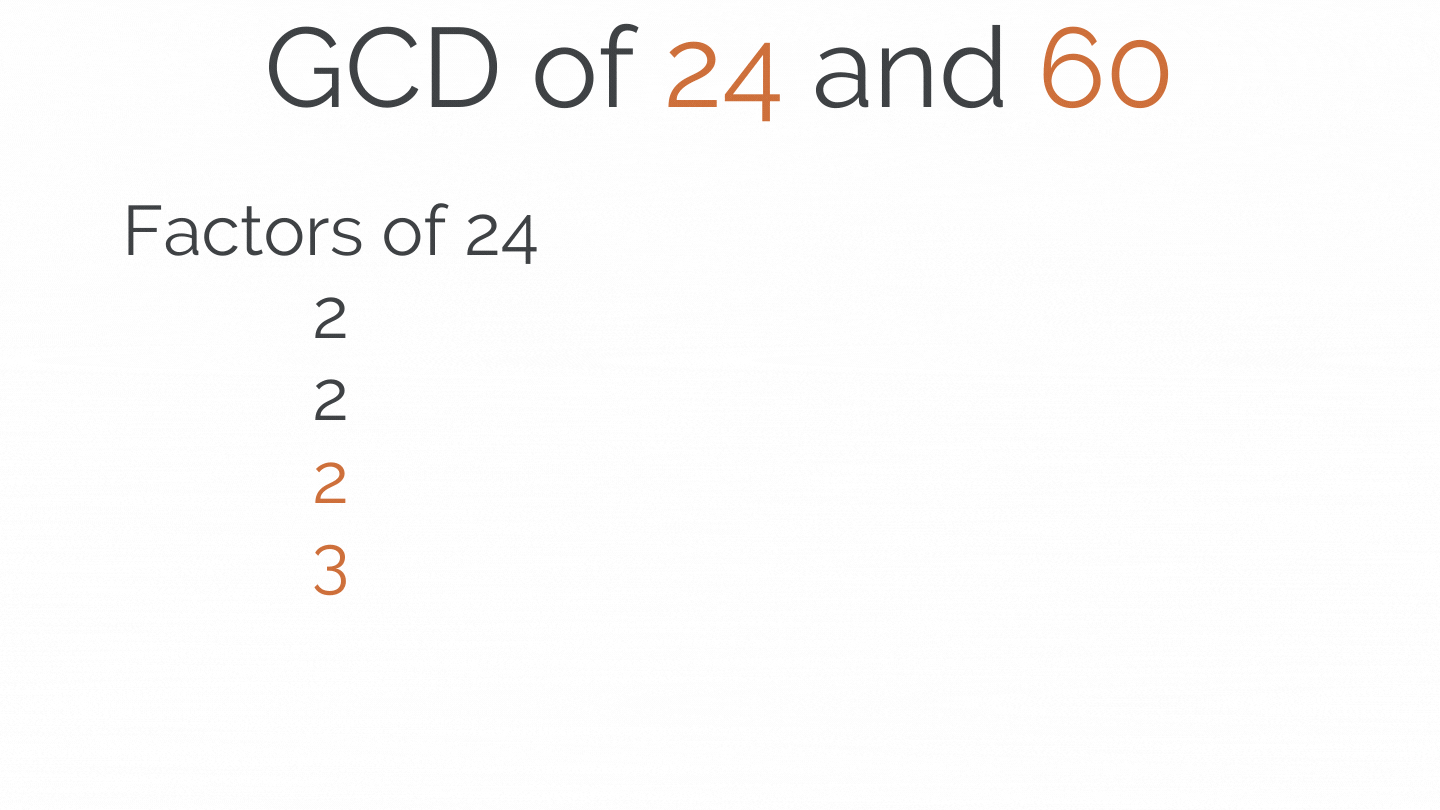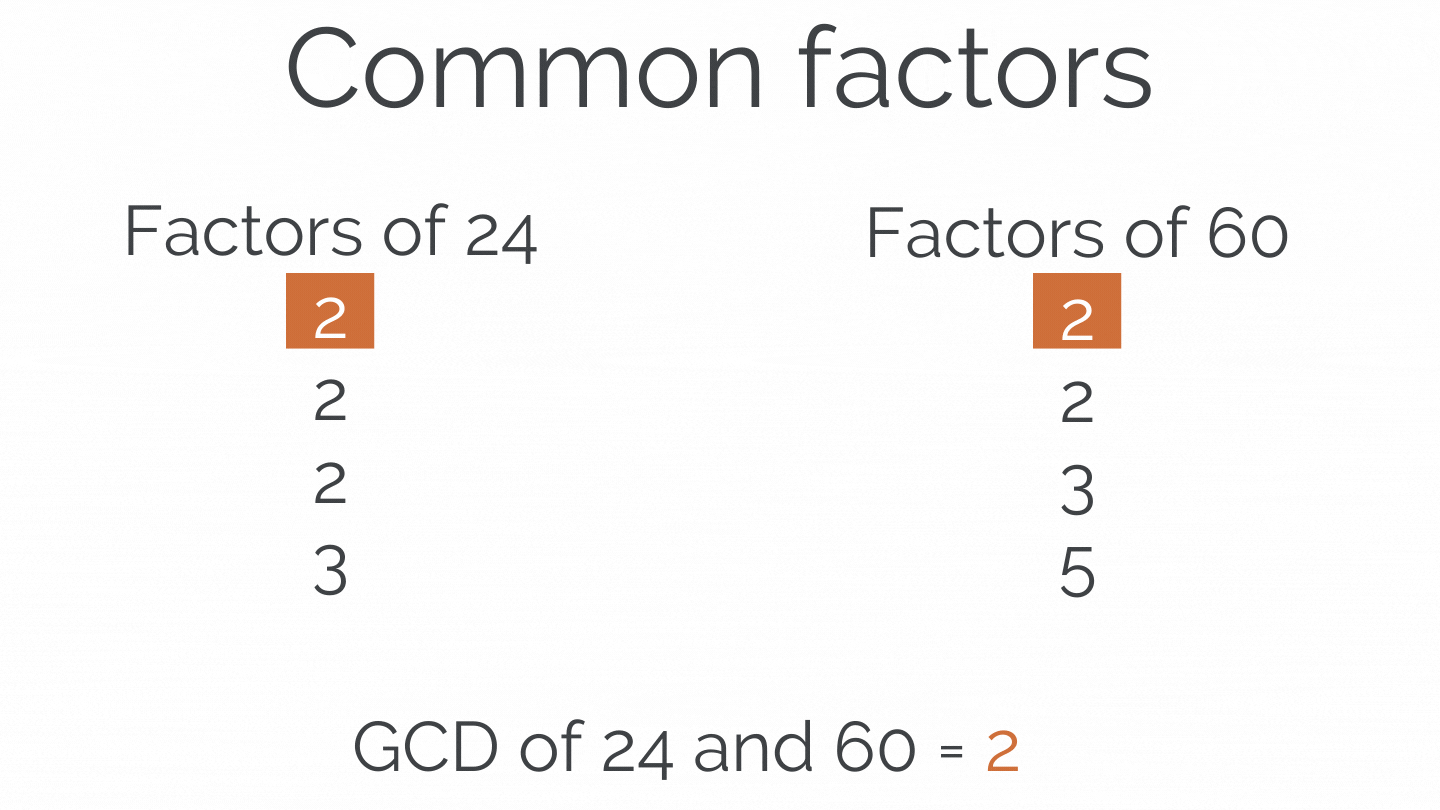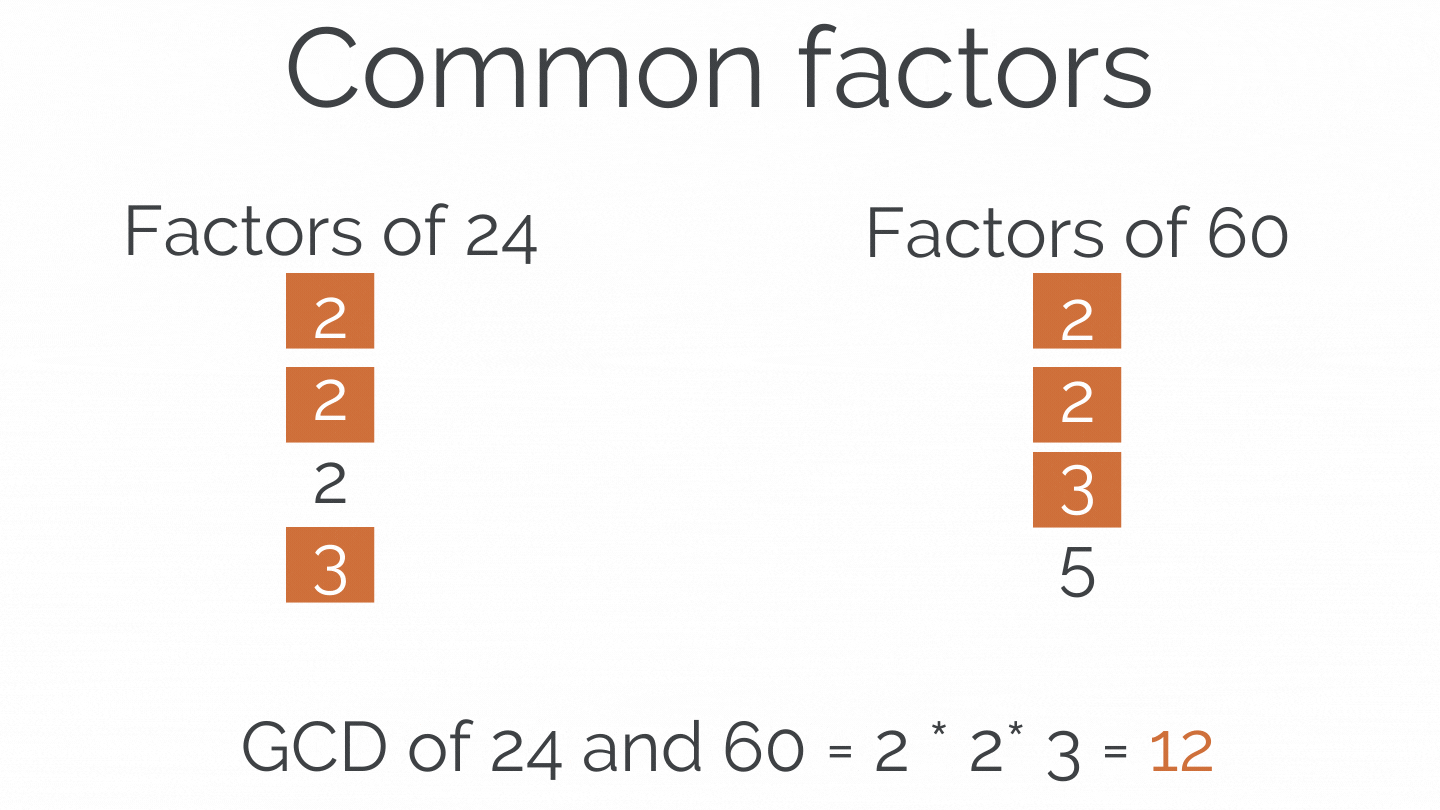
def GCD(a, b): low = min(a, b) high = max(a, b) if low == 0: return high elif low == 1: return 1 else: return GCD(low, high%low) print(GCD(24,60))

Merge Sort

The most efficient sorting algorithm is Merge sort. It works on the principle of Divide and Conquers. Merge sort repeatedly breaks down a list into several sublists until each sublist consists of a single element and merges those sublists in a manner that results in a sorted list.

def merge_sort(inp_arr): size = len(inp_arr) if size > 1: middle = size // 2 left_arr = inp_arr[:middle] right_arr = inp_arr[middle:] merge_sort(left_arr) merge_sort(right_arr) p = 0 q = 0 r = 0 left_size = len(left_arr) right_size = len(right_arr) while p < left_size and q < right_size: if left_arr[p] < right_arr[q]: inp_arr[r] = left_arr[p] p += 1 else: inp_arr[r] = right_arr[q] q += 1 r += 1 while p < left_size: inp_arr[r] = left_arr[p] p += 1 r += 1 while q < right_size: inp_arr[r] = right_arr[q] q += 1 r += 1 inp_arr = [8, 3, 5, 1, 2, 7, 6, 9] print("Input Array :\n") print(inp_arr) merge_sort(inp_arr) print("\n") print("Sorted Array :\n") print(inp_arr)

Tower of Hanoi

A mathematical puzzle where we have three rods and n disks is known as the Tower of Hanoi. Here the puzzle is to move the entire stack to another rod, obeying the following simple rules:

1. At a time, one disk can move.
2. It works by taking the upper disk from one stack and placing it on top of another stack, i.e., a disk can move if it is the uppermost disk on a stack.
3. A larger disk can not be put on top of a smaller disk.

Transferring the top n-1 disks from the source rod to the Auxiliary rod can again be thought of as a fresh problem and can be solved in the same manner.

def TowerOfHanoi(n, source, destination, auxiliary): if n == 1: print("Move disk 1 from source", source, "to destination", destination) return TowerOfHanoi(n - 1, source, auxiliary, destination) print("Move disk", n, "from source", source, "to destination", destination) TowerOfHanoi(n - 1, auxiliary, destination, source) n = 4 TowerOfHanoi(n, 'A', 'B', 'C')

Reverse a string

As per the title, it reverses the original string, i.e., modifying the original string and arranging it in a reverse manner, starting from the last character to the first character.

def reverse(string): if len(string) == 0: return string else: return reverse(string[1:]) + string[0] reverseme = 'Desserts' print(reverse(reverseme)) reverseme = 'Knits' print(reverse(reverseme)) reverseme = 'Regal' print(reverse(reverseme)) reverseme = 'Pupils' print(reverse(reverseme)) reverseme = 'Smart' print(reverse(reverseme)) reverseme = 'Pals' print(reverse(reverseme)) reverseme = 'Straw' print(reverse(reverseme)) reverseme = 'Time' print(reverse(reverseme)) reverseme = 'Star' print(reverse(reverseme))

If you like what we do and want to know more about our community 👥 then please consider sharing, following, and joining it. It is completely FREE.

Also, don’t forget to show your love ❤️ by clapping 👏 for this article and let us know your views 💬 in the comment. Join here: https://blogs.colearninglounge.com/join-us