Recursive Function Explained
If this is your first programming language then you must have been very confused with a recursive function. In this article, we will explain what a recursive function is with intuitive examples. Before we jump to the actual topic of the discussion. Let’s recap “What is Function?” in the programming language.
Consider a situation where the complexity of your python project increases; There’s a good chance that you will land yourself in a place where you have to write the same code repeatedly. Apart from the monotonous work we get after having repetitive coding blocks, it also results in our codebase with visual clutters. These codebases are prone to human error which eventually will lead us to the condition where we might need our code at multiple places, it can also become a blunder if try to add functionality to that process; henceforth all of these lead to an impossible unit or integration test 😤
For example, you want to multiply any two integer numbers. So rather than writing the same code repeatedly, we can package the code into the function.
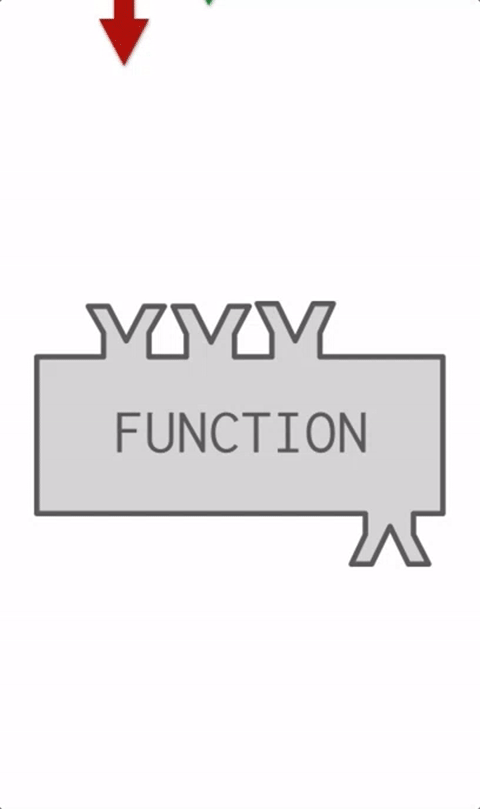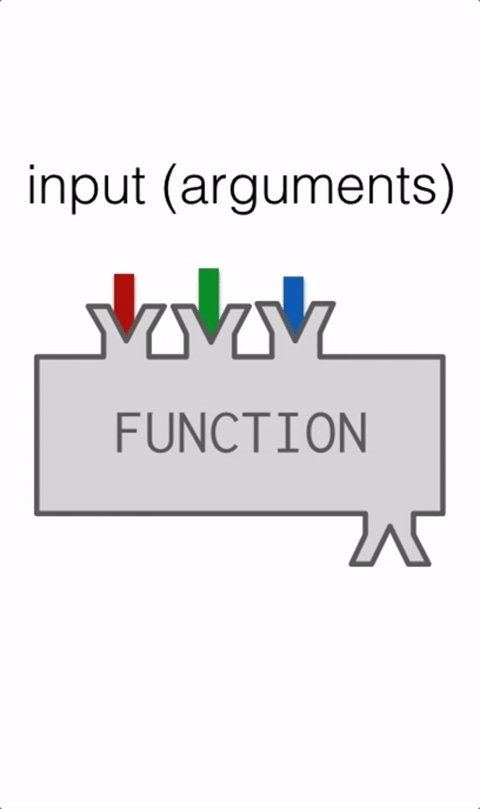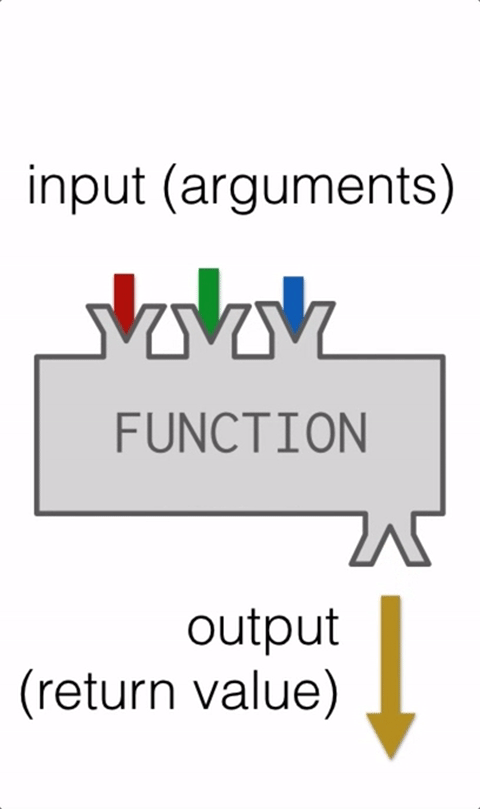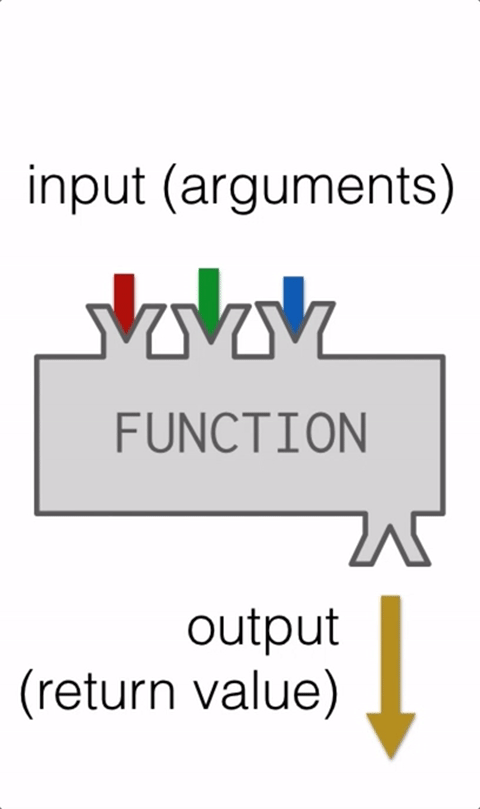
That is one of the mightiest features of Python programming. It has been often found that initially, it takes a bit of effort to get started with it, but once it has been done, it will change the complete outlook on how you code. For easier understanding, we break down the code into smaller chunks by creating functions. It also becomes a helping hand to program more efficiently and also makes you organize your code in a better way.
When to use functions?
If you are in the condition where you are writing the same code pattern more than once, you should probably think about investing some time into writing a function that you can reuse whenever it is needed. Use a function if you start to see that you need to write the same piece of code over and over. That’s what refactoring is!
Now consider writing the same multiplication function in Python. It looks something like this.

OK, So What is Recursion?
Recursion is a method for solving larger problems that can be broken down into smaller, repetitive problems. A method or function is recursive if it can call itself.
In layman, it looks like this,
A child couldn't sleep, so her mother told her a story about a little frog,
who couldn't sleep, so the frog's mother told her a story about a little bear,
who couldn't sleep, so the bear's mother told her a story about a little weasel...
who fell asleep.
...and the little bear fell asleep;
...and the little frog fell asleep;
...and the child fell asleep.If you have watched Inception, it is a film by Christopher Nolan starring Leonardo DiCaprio.
If you still haven’t got a chance to watch the movie, you are probably missing out once in a lifetime masterpiece, especially if you are in software engineering because it makes you THINK.
The concept of the movie is very similar to Recursion.
Recursion is simply a program calling itself until some condition is fullfilled.

DiCaprio, starring as Cobb, is a rather unusual thief who steals sensitive information from sleeping people. He gets into your dream and creates a fake reality that convinces you to share the information. The following is a code representation of this act — a simple function.

Cobb’s usual task, which is to obtain information from people, is easy-peasy, right?. But, how about ‘planting’ an idea on someone’s mind, so they think they created the idea? This is a serious challenge and takes going deeper and deeper into dreams. Yes, exactly — a dream inside a dream. And this is where Recursion is similar to the movie.

Now, let’s try to use our mult function and use it to implement the Factorial of a number.
Let’s take the example of Factorial (5 factorial is the product of all natural numbers up to 5 and is represented by 5! ),
Here’s how we find n!:
n!=n(n−1)!
Did you see that? To define n! we used factorial itself. Now (n−1)! can be defined as:
(n−1)!=(n−1)(n−2)!
In this way, we keep calling factorial until we reach 0! we give the value 1. This becomes :
n!=n(n−1)(n−2)..(1)
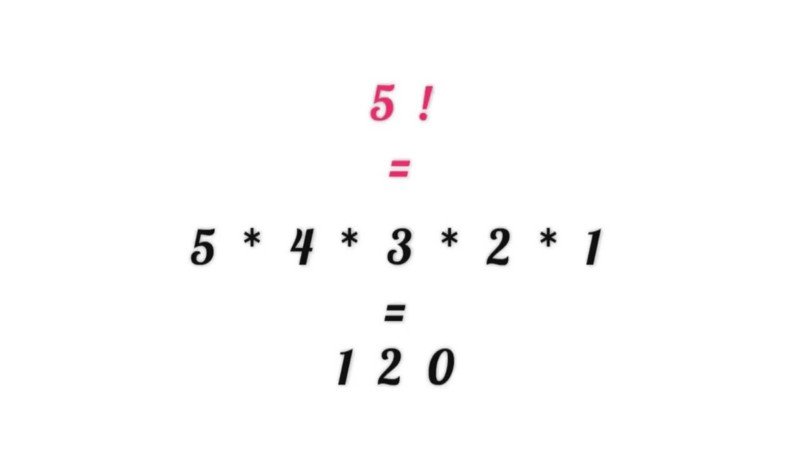
Take a pause and see if you can really use your mult function to implement recursion. As shown below, you can do it, but there is an efficient way to use a recursive function.

Factorial of number can be solved using recursion as we can calculate factorial of bigger numbers by calculating factorials of lower numbers. Here, a bigger task is broken into a smaller repetitive task that calculates the factorial of the next number.
fact(5) = 5 * fact(4) fact(5) = 5 * 4 * fact(3) fact(5) = 5 * 4 * 3 * fact(2) fact(5) = 5 * 4 * 3 * 2 * fact(1) fact(5) = 5 * 4 * 3 * 2 * 1
To be a recursive function, it needs to have the following condition.
Base Case: This is a condition that when satisfied stops the recursion. In our case, the base case (or exit condition) is that 0! = 1
Recursive Case: This is where the function calls itself.
First, let’s define our Base case in Python. Here, our base case is 0! = 1 where the function should stop.

Now here’s the recursive part,

Loops Vs. Recursion
Recursion might sound exactly the same as loops but both are very much distinct.
Iteration is used to perform a repetitive block of code as many times as necessary for the program. In contrast, Recursion can solve all those problems that a loop can solve. But it is difficult or quite impossible to solve some problems by for loop. A big difference between Recursion and iteration lies in the way that they end. Whereas a loop executes a block of code by checking each time if it has reached the end of the sequence, on the other hand, there are no defined sequential ends for recursive code.
When to use(or not to) use Recursion?
Use Recursion, if and only if the larger problem can be broken down into a small problem that needs to call itself. A single base case is an absolute necessity to have when using recursive functions to make it stop calling itself or raise a RecursionError: maximum recursion depth exceeded in comparison.
Why do we use recursive function calls?
- They are often easier to understand.
- A lot of interesting algorithms use a divide-and-conquer approach.
- Some languages do not have looping constructs, or the constructs are awkward to use.
- Dynamic programming solutions can often be rewritten to be recursive with memoization.
- If an algorithm has to use an explicit stack (LIFO) then using the call stack has minimal impact on the memory footprint.
- The risk is that many operating systems and language runtimes have strict limits on stack size versus heap size.
Now we’ve learned what a recursive function is and how it is distinct from looping statements and regular functions. Moreover, recursion can be viewed as a subtle fundamental programming method that can serve you well both in coding competitions and “real world” programming. It’s commonly used in trees, but other functions can be written with recursion to provide elegant solutions.
If you like what we do and want to know more about our community 👥 then please consider sharing, following, and joining it. It is completely FREE.
Also, don’t forget to show your love ❤️ by clapping 👏 for this article and let us know your views 💬 in the comment.
Join here: https://blogs.colearninglounge.com/join-us
